
randomized_select에 이어서 다른 select 알고리즘을 배웠는데. 요놈은 random으로 pivot을 설정하는 대신 다른 방법으로 pivot을 설정하여서 Select를 진행한다.
내가 이해한 바에 의하면 1번줄부터 10번째 줄까지는 배열에 있는 숫자가 5로 나눠떨어지지 않으면 가장 작은 놈을 찾아서 배열에서 퇴출시킨다. 아주 잔인한 놈들...
1-4번까지가 가장 작은놈을 찾아서 맨앞으로 가지고 오는것이고 9-10번을 보시면 한명을 퇴출시킬수록 p(시작점)을 하나씩 증가시키고 i 찾으려고 하는 넘의 수를 하나씩 줄인다(내가 조직에서 4번째로키가 컷는데 맨 작은놈이 나가버리면 3번째가 되는 논리)
그렇게 줄이다가 조직원의 수가 5로 나누어 떨어지면 반복문이 종료되거나, 그렇게 반복문 실행중에 i가 1이 되버리면 그 A[p] (그 반복 시점에서 가장 첫번째값)을 리턴한다.
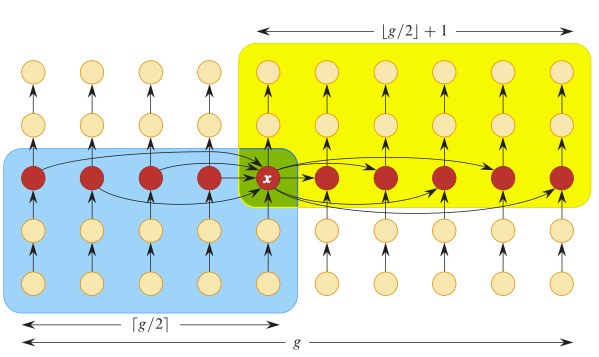
그렇다 그렇게 5로 나누어 떨어지게 되면 위에처럼 5로 나누어서 g개의 그룹을 얻게되는데.... 지금 여기 그림에서는 g가 10이다(열이 10개니까)
12-13줄을 보면 열에 따라서 정렬을 하고 있는걸 볼수있다(위로 가는 화살표 방향)
그렇게 되면 각 열의 중앙값(median)이 빨간색이 되게 되는데
그 빨간색들에 대해서 다시 select을 재귀호출해서 select(A, p+2g, p+3g-1, 아니 이건 쓰는 기호가 없네) 16번째 줄 보세요.(결국 빨간 점들중 가장 왼쪽이 p+2g, p+3g-1, 그것의 중앙값 인덱스를 넣어서 select을 하는거...)
그렇게 되면 전체 배열의 찐찐 찐이야~ 중앙값을 갖게 될 수 있다.(여기 그림에서는 x)
자 그럼 우리가 처음 구하고자 했던 중앙값의 인덱스를 구하기 위해서 다시 17번째 줄에서 partition_around를 적용하면 요놈 보다 작은놈은 앞으로 큰놈은 뒤로 보내서 이놈의 인덱스를 구할수 있고, 그 인덱스를 반환해서 우리가 구하고싶은 i번재로 큰 값의 i 랑 비교를 했을때 운 좋게 같으면 그놈 바로 리턴.
인생이 그리 쉽지 않지. 크거나 작다면 ... 다시 재귀호출인데
우리가 구한 인덱스가 구하고자 하는 i보다 크다면 q 포함 큰 부분은 다 날리니까 select(A, p, q-1, i)
반대로 우리가 구한 인덱스가 구하고자 하는 i 보다 작다면, q 포함 작은부분은 다 날리니까 select(A, q+1, r, i-k)
여기서 앞에꺼 빼주니까 빼주는 만큼 i에서 k를 빼주는 거 잊지 않기! ( 반에서 나보다 작은놈들 3명 전학가면 그만큼 내 키 순위도 낮아지는 원리)
randomized select은 무작위로 pivot을 선출하여서 확률적으로 최악의 시간복잡도를 피하려고 했다면
이 select 알고리즘은 어떻게든 안정적으로 pivot을 뽑기따위는 안하것어! 정렬시켜 탁탁, 기준 5로 세워! 해서 구하는 느낌이다.